数据结构代码题

线性表

顺序表

基本操作

初始化

#define MaxSize 10;	//定义最大长度
typedef struct{
	int data[MaxSize];	//静态数组存储数据元素
    int length;			//当前长度
}SqList;

void InitList(SqList &L){
    for(int i=0;i<MaxSize;i++)
        L.data[i]=0;
    L.length=0;
}

#define InitSize 10
typedef struct{
    int *data;		//指示动态分配数组的指针
    int MaxSize;	//顺序表的最大容量
    int length;		//顺序表的当前长度
}SqList;

void InitList(SeqList &L){
    L.data=(int *)malloc(InitSize*sizeof(int));	//分配存储空间
    L.length=0;			//顺序表初始长度为0
    L.MaxSize=InitSize;	//初始化存储容量
}

插入操作

bool ListInsert(SqList &L,int i,int e){
	if(i<1||i>L.length+1)	//判断插入位置是否有效
        return false;
    if(L.length>=MaxSize)	//若存储空间已满
        return false;	
    for(int j=L.length-1;j>=i-1;j--) //第i个元素，以及其后面的元素后移
        L.data[j+1]=L.data[j];
    L.data[i-1]=e;
    L.length++;
    return true;
}

删除操作

bool ListDelete(SqList &L,int i){
	if(i<1||i>L.length)
        return false;
    e=L.data[i-1];
    for(int j=i;j<L.length;j++)
        L.data[j-1]=L.data[j];
    L.length--;
    return true;
}

按值查找

int LocationElem(SqList L,int e){
	int i;
    for(i=0;i<L.length;i++)
        if(L.data[i]==e);
    		return i+1;	//返回其位序
    return 0;	//未找到
}

题

从顺序表中删除具有最小值的元素(假设唯一)并由函数返回被删元素的值。空出的位置由最后一个元素填补，若顺序表为空，则显示出错信息并退出运行。

typedef struct{
    int *data;
    int MaxSize;	//顺序表最大容量
    int length;		//当前长度
}SqList;

bool delete_min(SqList &L,int &e){	//注意引用参数也要添加&
	if(L.length==0)
        return false;
    int min=L.data[0];
    int x=0;
    for(int i=0;i<L.length;i++){
        if(L.data[i]<min){
            min=L.data[i];
            x=i;
        }
    }
    e=L.data[x];
    L.data[x]=L.data[L.length-1];
    L.length--;
    retrun true;
}

将顺序表L的所有元素逆置，空间复杂度为O(1)

typedef struct{
	int *data;
    int MaxSize;
    int length;
}SqList;

void Reverse(SqList &L){
    int t;
    for(int i=0;i<L.length/2;i++){
        t=a[i];
        a[i]=a[L.length-1-i];
        a[L.length-1-i]=t;
    }
}

对长度为n的顺序表L，编写一个算法删除顺序表中所有值为x的数据元素，要求时间复杂度为O(n)、空间复杂度为O(1)。

//记录下不等于x的值，将不等于x的值放到下标k的位置。k是不等于x的个数-1.
typedef struct{
    int *data;
    int MaxSize;
    int length;
}SqList;
	
void delete_x(SqList &L,int x){
	int k=0;
	for(int i=0;i<L.length;i++){
		if(L.data[i]==x)
            k++;
        else
            L.data[i-k]=L.data[i];
	}
    L.length=L.length-k;
}

从顺序表中删除值在s和t之间的所有元素(包含s和t，要求s<t)。若s或t不合理或顺序表为空，则显示出错并退出。

bool delete_s_t(SqList &L,int s,int t){
    int i,k=0;
    if(s>=t||L.length==0)
        return false;
    for(i=0;i<L.length;i++){
        if(L.data[i]>=s&&L.data[i]<=t)
            k++;
        else
            L.data[i-k]=L.data[i];
    }
    L.length=L.length-k
    return true;
}

从有序顺序表中删除其值重复的元素，使表中所有元素的值不同

void delete_Same(SqList &L){
    int k=0;	
    for(int i=1;i<L.length;i++)		
        if(L.data[k]!=L.data[i])
            L.data[++k]=L.data[i];
    L.length=k+1;
}

将两个有序顺序表合并为一个新的有序顺序表，并由函数返回结果顺序表

bool merge(SqList &A,SqList &B,SqList &C){
	int i=0,j=0,k=0;
    while(i<A.length&&j<B.length){
        if(A.data[i]<B.data[j])
            C.data[k++]=A.data[i++];
        else
            C.data[k++]=B.data[j++];
    }
    if(i<A.length)
		C.data[k++]=A.data[i++];
    else
         C.data[k++]=B.data[j++];
    C.length=k;
    return true;
}

在一位数组A[m+n]中依次存放两个线性表。编写一个算法将两个顺序表位置互换。

void Reverse(int A[],int left.int right){
    int mid=(left+right)/2;
    int t;
    for(int i=0;i<=mid-left;i++){
        t=A[left+i];
        A[left+i]=A[right-i];
        A[right-i]=t;
    }
}

void Exchange(int A[],int m,int n){
    Reverse(A,0,m+n-1);
    Reverse(A,0,n-1);
    Reverse(A,m,n+m-1);
}

线性组a1,a2…,an中的元素递增有序，按顺序存储。设计一个算法，用最少时间查找表中为x的元素，若找到，则将其与后继元素互换。若找不到，则将其插入表中并使表中元素仍递增有序。

//折半查找
void Search(int A[],int x){
    int low=0,high=n-1,mid;
    while(low<=high){
        mid=(low+high)/2;
        if(A[mid]==x)
            break;
        else if(A[mid]<x)
            low=mid+1;
        else
            high=mid-1;
    }
    if(A[mid]=x&&mid!=n-1){
        t=A[mid];
        A[mid]=A[mid+1];
        A[mid+1]=t;
    }
    if(low>high){
        for(i=n-1;i>high;i--)
            A[i+1]=A[i];
        A[i+1]=x;
    }
}

给定三个序列A、B、C，长度均为n，且均为无重复元素的递增序列，请设计一个时间上尽可能高效的算法，逐行输出同时存在于这三个序列中的所有元素。例如，数组A为{1,2,3]，数组B为{2,3,4]，数组C为{-1,0,2}，则输出2。

void Search(int A[],int B[],int C[],int n){
    int i=0.j=0.k=0;
    while(i<n&&j<n&&k<n){
        if(A[i]==B[j]&&B[j]==C[k]){
            printf("%d\n",A[i]);
            i++;
         	j++;
            k++;
        }else{
            int maxNum=max(A[i],max(B[j],C[k]));
            if(A[i]<maxNUm) i++;
            if(B[i]<maxNUm) j++;
            if(C[i]<maxNUm) k++;
        }
    }
}

将数组A中的序列循环左移p个位置，数组长度为n

void Reverse(int A[],int left.int right){
    int mid=(left+right)/2;
    int t;
    for(int i=0;i<=mid-left;i++){
        t=A[left+i];
        A[left+i]=A[right-i];
        A[right-i]=t;
    }
}

void Reverse_left(int A[],int n,int p){
    Reverse(R,0,p-1);
    Reverse(R,p,n-1);
    Reverse(R,0,n-1);
}

​

链表

typdef struct LNode{
    int data;
    struct LNode *next;
}LNode,*LinkList;

单链表

基本操作

求表长

int Length(LinkList L){
	int len=0;
    LNode *p=L->next;	//指向链表的第一个元素
    while(p!=null){
        p=p->next;
        len++;
    }
    return len;
}

按序号查找

LNode *GetElem(LinkList L,int i){
	LNode *p=L;
    while(i!=0&&p!=NULL){
        p=p->next;
        i--;
    }
    return p;
}

插入结点

//后插法
bool LinkInsert(LinkList &L,int i,int e){	//在第i个结点的位置插入数据e
	LNode *p=L;
    while(p!=NULL&&i!=1){	//找到第i个结点的前驱
        p=p->next;	
        i--;
    }
    if(p==NULL)
        return false;
    LNode *s=(LNode*)malloc(sizeof(LNode));
    s->data=e;
    s->next=p->next;
    p->next=s;
    return true;
}

//前插法
bool LinkInsert(LinkList &L,LNode *p,int e){	//将数据e插入到结点p之前
    LNode *s=(LNode*)malloc(sizeof(LNode));
    s->next=p->next;
    p->next=s;
    //将前插法转换为后插法，只需要交换两个结点的数据的元素
    s->data=p->data;
    p->data=e;
}

删除结点

//删除第i个结点
bool ListDelete(LinkList &L,int i,int e){
	LNode *p=L;
    while(p!=NULL&&i!=1){
        p=p->next;
        i--;
    }
    if(p==NULL||p->next=NULL)
        return false;
    LNode *q=p->next;	//删除结点
    p->next=q->next;
    free(q);
    return true;
}

//可以删除p的后继来完成操作
q=p->next;
p->data=q->data;
p->next=q->next;
free(q);

头插法建表

//头插法建立的链表的逆序的
LinkList Creat(LinkList &L){
	LNode *s;
    int x;
    L=(LNode *)malloc(sizeof(LNode));
    L->next=NULL;
    scanf("%d",&x);
    while(x!=9999){
        s=(LNode *)mallocf(sizeof(LNode));
        s->data=x;
        s->next=L->next;
        L->next=s;
        scanf("%d",&x);
    }
    return L;
}

尾插法建表

//尾插法建立的链表的顺序的
LinkList Creat(LinkList &L){
    L=(LNode *)malloc(sizeof(LNode));
    LNode *s;
    LNode *tail=L;
    int x;
    scanf("%d",&x);
    while(x!=9999){
        s=(LNode *)malloc(sizeof(LNode));
        s->data=x;
        tail->next=s;
        tail=s;
        scanf("%d",&x);
    }
}

例题

1.带有表头结点的单链表，结点结构为data、link
假设该链表只给出了头指针 list。在不改变链表的前提下，请设计一个尽可能高效的算法，查找链表中倒数第k个位置上的结点(k为正整数)。若查找成功，算法输出该结点的 data 域的值，并返回1:否则，只返回0。要求:
1)描述算法的基本设计思想
2)描述算法的详细实现步骤
3)根据设计思想和实现步骤，采用程序设计语言描述算法(使用C、C++或 Java 语言实现)，关键之处请给出简要注释。

1.先遍历链表，计算出链表的长度，倒数第k个元素就是n-k+1个元素;
typedef struct LNode{
    int data;
    struct LNode *link;
}LNode,*LinkList;

int function(LikeList &L,int k){
    int count=0;
    LNode *p=L->link;
    while(p!=null){
        p=p->next;
        count++;
    }
    for(int i=0;i<count-k+1;i++){
        p=p->next;
    }
    printf("%d",p->data);
}

2.假定采用带头结点的单链表保存单词，当两个单词有相同的后缀时，可共享相同的后缀存储空间，例如，loading和being的存储映像如下图所示。

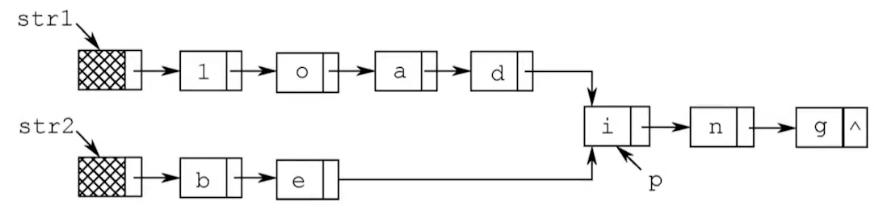
设 str1和 str2 分别指向两个单词所在单链表的头结点，链表结点结构为data，next请设计一个时间上尽可能高效的算法，找出由str1和str2 所指向两个链表共同后缀的起始位置(如图中字符i所在结点的位置p)。要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++或 Java语言描述算法，关键之处给出注释
3)说明你所设计算法的时间复杂度。

typdef struct LNode{
    int data;
    struct LNode *next;
}LNode,*LinkList;

int function(LinkList &str1,LinkList &str2){
    int count1=0;
    int count2=0;
    LNode *p=str1->next;
    LNode *q=str2->next;
    while(str1!=null){
        p=p->next;
        count1++;
    }
    while(str2!=null){
        q=q->next;
        count2++;
    }
    int x=count1-count2;
    int t=count2;
    if(count2>count1){
        p=str2->next;
        q=str1->next;
        t=count1;
    }
    for(int i=0;i<x;i++)
        q=q->next;
    for(int i=0;i<t;i++){
        if(q==p)
            return p;
        q=q->next;
        p=p->next;
    }
}

3.在带头结点的单链表L中，删除所有值为x的结点，并释放其空间，假设值为x的结点不唯一，编写算法实现上述操作。

//删除/插入结点——可考虑前后指针
typdef struct LNode{
    int data;
    struct LNode *next;
}LNode,*LinkList;

void delete_x(LinkList &L,int x){
    LNode *pre=L;
    LNode *p=L->next;
    while(p!=null){
        if(p->data==x){
            LNode *q=p;
            p=p->next;
            pre->next=p;
            free(q);
        }else{
            pre=p;
            p=p->next;
        }
    }
}

4.在一个关键字递增有序的单链表中插入新关键字x，需确保插入后单链表保持递增有序。

typdef struct LNode{
    int data;
    struct LNode *next;
}LNode,*LinkList;

void insert_x(LinkList &L,int x){
    LNode *pre=L;
    LNode *p=L->next;
    while(p!=null){
        if(p->data>x){
            break;
        }else{
            pre=p;
            p=p->next;
        }
    }
    LNode *q=(LNode *)malloc(sizeof(LNode));
    q->data=x;
    q->next=p;
    pre->next=q;
}

5.用单链表保存m个整数，结点的结构为[data] [link]，且|data|<n(n 为正整数)。现要求设计一个时间复杂度尽可能高效的算法，对于链表中 data 的绝对值相等的结点，仅保留第一次出现的结点而删除其余绝对值相等的结点。
例如

要求:
1)给出算法的基本设计思想。
2)使用C或 C++语言，给出单链表结点的数据类型定义。
3)根据设计思想，采用C或C++语言描述算法，关键之处给出注释
4)说明你所设计算法的时间复杂度和空间复杂度。

1.建立一个数组A，遍历链表，对链表中出现的元素，则在对应的数组下标中让数组元素加1。统计出现次数。
  重新遍历链表，若对应的数组中元素大于1，则删除该结点。
typdef struct LNode{
    int data;
    struct LNode *next;
}

void function(LinkList &L){
    int A[n+1];
    for(int i=0;i<=n;i++){
        A[i]=0;
    }
    LNode *p=L->next;
    LNode *pre=L;
    
    while(p!=null){
        int x=p->data;
        if(x<0)
            x=x*-1;
        A[x]++;
        p=p->next;
    }
    p=L->next;
    
    while(p!=null){
        int x=p->data;
        if(x<0)
            x=x*-1;
        if(A[x]>1){
            LNode *q=p;
            p=p->next;
            pre->next=p;
            free(q);
        }else{
            pre=p;
            p=p->next;
        }
    }  
}

6.试编写算法将带头结点的单链表就地逆置，所谓“就地”是指辅助空间复杂度为 O(1)。

void ListReserve(Linklist &L){
    LinkList head=(LNode *)malloc(sizeof(LNode));
    head->next==null;
    
    while(L->next!=null){
        Lnode *p=L->next;
        L->next=L->next->next;
        p->next=head->next;
        head->next=p;
    }
    
    L->next=head->next;
    free(head);
}

7.{a1,b1, a2,b2,…,an,bn}为线性表，采用带头结点的单链表存放，设计一个就地算法，将其拆分为两个线性表，
使得A={a1,a2,…,an}，B={bn,…,b2, b1 }。

//对a进行尾插法，对b进行头插法
LinkList function(LinkList &L){
    LinkList A=(LNode *)malloc(sizeof(LNode));
    LinkList B=(LNode *)malloc(sizeof(LNode));
    A->next=null;
    B->next=null;
    int count=0;	//判断是奇数位置还是偶数位置
    LNode *tailA=A;	//tailA指向A的链尾 
    while(L->next!=null){
        count++;
        LNode *p=L->next;
        L->next=L->next->next;
        if(count%2!=0){
            tailA->next=p;
            p->next=null;
            tailA=p;
        }else{
            p->next=B->next;
            B->next=p;
        }
    }
}

8.设线性表L=(a1,a2,a3,…,an-2,an-1,an)采用带头结点的单链表保存，链表中的结点定义如下:

请设计一个空间复杂度为 0(1)且时间上尽可能高效的算法，重新排列工中的各结点，得到线性表L=(a1,an,a2,an-1,a3,an-2)。要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释
3)说明你所设计的算法的时间复杂度。

//前一半元素尾插法，后一半元素头插法

双链表

基本操作

typedef struct DNode{
    int data;
    struct DNode *prior,*next;
}DNode,*DLinkList;

插入结点

//在p结点后插入s结点
bool InsertNextDNode(DNode *p,DNode *s){
    if(p==NULL||s==NULL)    //非法参数
        return false;
    s->next=p->next;    //将s插入到p结点之后
    if(p->next!=NULL)    //如果p结点有后继节点
        p->next->prior=s;
    s->prior=p;
    p->next=s;
}

删除结点

//删除p结点的后继节点
bool DeleteNextDNode(DNode *p){
    if(p==NULL)
        return false;
    DNode *q = p->next;     //找到p的后继结点q
    if(q==NULL)     //p没有后继
        return false;
    p->next=q->next;
    if(q->next!=NULL)   //q不是最后一个结点
        q->next->prior=p;
    free(q);    //释放结点
    return true;
}

销毁双链表

//销毁双链表
void DestoryList(DLinkList &L){
    //循坏释放各个数据结点
    while(L->next!=NULL)
        DeleteNextDNode(L);
    free(L);    //释放头结点
    L=NULL;     //头指针指向NULL
}

静态链表

#define MaxSize 10
typedef struct{
	int data;   //存储数据元素
    int next;   //下一个元素的数组下标
}SLinkList[MaxSize];

栈

顺序栈

#definde MaxSize 50
typedef struct{
    int data[MaxSize];
    int top;
}SqStack;

基本操作

初始化

void InitStack(SqStack &S){
	S.top=-1;
}

栈判空

bool StackEmpty(SqStack S){
    if(S.top==-1)
        return true;
    else
        return false;
}

进栈

bool Push(SqStack &S,int x){
    if(S.top==MaxSize-1)
        return false;
    S.data[++S.top]=x;	//先加后入
    return true;
}

bool Push(SqStack &S,int x){
    if(S.top==MaxSize)
        return false;
    S.data[S.top++]=x;	//先入后加
    return true;
}

出栈

bool PoP(SqStack &S,int x){
    if(S.top==-1)
        return false;
    x=S.data[S.top--];	//先出后减
    return true;
}

bool PoP(SqStack &S,int x){
    if(S.top==0)
        return false;
    x=S.data[--S.top];	//先减后出
    return true;
}

队列

#define MaxSize 50
typedef struct{
    int data[MaxSize];
    int front;
    int rear;
}SqQueue;

串

基本操作

求子串

//返回串S的第pos个字符起长度为len的子串
#define MAXLEN 255
typedof struct{
    char ch[MaxLen];
    int length;
}SString;

bool SubString(SString &Sub, SString S, int pos, int len){
    if(pos+len-1>S.length)
        retrun false;
    for(int i=pos;i<len;i++){
        int j=1;
        Sub.ch[j]=S.ch[i];
        j++;
    }
    Sub.length=len;
    return true;
}

比较串

//若S>T，则返回值>0；若S=T，则返回值=0；若S<T，则返回值<0 
bool StrCompare(SString S, SString t){
    for(int i=1;i<S.length && i<T.length;i++){
        if(S.ch[i]!=T.ch[i])
            return S.ch[i]-T.ch[i];
    }
    //若前缀相同，串长的更大
    return S.length-T.length;
}

定位串

//若主串S中存在与串T值相同的子串，则返回它在主串S中第一个出现的位置；否则函数值为0
int Index(SString S, SString T){
    int i=1, n=StrLength(S), m=StrLength(T);
    SString sub;	//用于暂存子串
    while(i<=n-m+1){
        SubString(sub,S,i,m);
        if(SubCompare(sub,T)!=0) i++;
        else retrun i;	//返回字串位置
    }
    return 0;	//S中不存在子串T
}

朴素模式匹配算法

int Index(SString S,SString T){
    int i=1,j=1;
    while(i<=S.length && j<-T.length){
        if(S.ch[i]==T.ch[i]){
            i++;
            j++;
        }else{
            i=i-j+2;
            j=1;
        }
    }
    if(j>T.length)
        return i-T.length;
    else 
        return 0;
}

KMP算法

int Index_KMP(SString S,SString T,int next[]){
	int i=1,j=1;
    while(i<=S.length && j<=T.length){
        if(j==0||S.ch[i]==T.ch[j]){
            ++i;++j;
        }
        else
            j=next[j];
    }
    if(j>T.length)
        return i-T.length;
    else 
        return 0;
}

if(T.ch[next[j]]==T.ch[j])
	nextval[j]=nextval[next[j]];
else
    nextval[j]=next[j];

树

基础代码

1.二叉链表数据结构

typedef struct BiTNode{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

2.双亲表示法

#define Max 100;
typedef struct{
    int data;
    int parent;
}BiTNode;

typedef struct{
    BiTNode nodes[Max];	
    int n;				//结点总数
}BiTree;

3.孩子兄弟表示法

typedef struct BiTNode{
	int data;
    struct BiTNode *child,*cousin;
}BiTNode,*BiTree;

4.孩子表示法

struct CTNode{
    int data;			//孩子结点在数组中的位置
    struct CTNode *next;//下一个孩子
};

typdef struct CTBox{
    int data;
    struct CTNOde *firstchild;	//第一个孩子
}CTBox;

typdef struct{
    CTBox nodes[MAX_TREE_SIZE];
    int n,r;			//结点数和根的位置
}CTree;

二叉树

typedef struct BiTNode{
	int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

基本操作

遍历

先序遍历

void PreOrder(BiTree T){
    if(T==NULL)
        return;
    visit(T);				//访问根节点
    PreOrder(T->lchild);	//递归遍历左子树
    PreOrder(T->rchild);	//递归遍历右子树
}

中序遍历

void PreOrder(BiTree T){
    if(T==NULL)
        return;
    PreOrder(T->lchild);	//递归遍历左子树
    visit(T);				//访问根节点
    PreOrder(T->rchild);	//递归遍历右子树
}

后序遍历

void PreOrder(BiTree T){
    if(T==NULL)
        return;
    PreOrder(T->lchild);	//递归遍历左子树
    PreOrder(T->rchild);	//递归遍历右子树
    visit(T);				//访问根节点
}

层序遍历

void LevelOrder(BiTree T){
	InitQUeue(Q);		//初始化队列
	BiTree p;		
	EnQueue(Q,T);		//将根节点入队
	while(!IsEmpty(Q)){	//队列不空则循环
		DeQueue(Q,p);	//队头结点出队
		visit(p);		//访问出队结点
		if(p->lchild!=null)
			EnQueue(Q,p->lchild);	//左子树不空，则左子树根节点入队
		if(p->rchild!=null)
			EnQueue(Q,p->rchild);	//右子树不空，则右子树根节点入队
	}
}

求二叉树高度

typedef struct BiTNode{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int height=0;

void ProOrder(BiTree T,int n){
    if(T==null)
        return;
    if(n>height)
        height=n;
    ProOrder(T->lchild,n+1);
    ProOrder(T->rchild,n+1);
}

int height(BiTree T){
    if(T==null)
        return 0;
    else
    	PreOrder(T,1);
    return height;
}

typedef struct BiTNode{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int PostOrder(BiTree T){
    if(T==null)
        return 0;
    int l=ProOrder(T->lchild);
    int r=ProOrder(T->rchild);
    if(l>r)
        return l+1;
    else
        return r+1;
}

求宽度

typedef struct BiTNode{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
int width[MAX];
//先序遍历，同时统计各层结点数
void PreOrder(BiTiree T,int level){
    if(T==null) return;
    width[level]++;
    PreOrder(T->lchild,level+1);
    PreOrder(T->rchild,level+1);
}
//求树宽度
int treeWidth(BiTree T){
    for(int i=0;i<Max;i++)		//初始化数组
        width[i]=0;
    PreOrder(T,0);
    int maxWidth=0;
    for(int i=0;i<Max;i++){
        if(width[i]>maxWidth)
            maxWidth=width[i];
    }
    return maxWidth;
}

求WPL

typedef struct BiTNode{
	int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
int WPL=0;

void PreOrder(BiTree T,int n){
    if(T==null) return;
    if(T->lchild==null&&T->rchild==null)
        WPL=WPL+T->weight*n;
    PreOrder(lchild,n+1);
    PreOrder(rchild,n+1);
}
int TreeWeight(BiTree T){
    PreOrder(T,0);
    return WPL;
}

判断是否为二叉排序树

//利用中序遍历，检查中序遍历得到的遍历序列是否递增
typedef struct BiTNode{
	int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int temp=Min_int; //记录以访问过的最大值
bool flag=true;

void InOrder(BiTree T){
    if(T==null) return;
    InOrder(T->lchild);
    
    if(T->data>=temp)
        temp=T->data;
    else
        flag=false;
    
    InOrder(T->rchild);
}	

判断二叉树是否平衡

//利用后序遍历
typedef struct BiTNode{
	int weight;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int PostOrder(BiTree T){
    if(T==null) return 0;
    int l=PostOrder(T->lchild);
    int r=PostOrder(T->rchild);
    
    if(left-right>1)  flag=false;
    if(left-right<-1) flag=false;
    
    if(left>right)
        return left+1;
    else
        return right+1;
}

判定是否为完全二叉树

//利用层序遍历
bool isComplete=true;	//是否为完全二叉树
bool flag=false;		//flag=true,表示层序遍历时出现过的叶子或只有左孩子的分支结点

void visit(BiTNode *p){
    if(p->lchld==null && p->rchil==null)	falg=true;
    if(p->lchld==null && p->rchil!=null)	isComplete=false;
    if(p->lchild!=null && p->rchild==null){
        if(flag) isComplete=false;
        flag=true;
    }
    if(p->lchild!=null && p->rchild!=null)
        if(flag) isComplete=false;
}

void LevelOrder(BiTree T){
    Queue Q;
    InitQueue(Q);
    BiTree p;
    EnQueue(Q,T);
    
    while(!isEmpty(Q)){
        DeQueue(Q,p);
		visit(p);
        if(p->lchild!=null)
        	EnQueue(Q,P->lchild);
        if(p->rchild!=null)
        	EnQueue(Q,p->rchild);
    }
}

例题

并查集

#define SIZE 3
int UFSets[SIZE];	//集合元素数组
//初始化并查集
void Initial(int S[]){
    for(int i=0;i<SIZE;i++){
        S[i]=-1;
    }
}
//Find“查”操作，找x所属集合（返回x所属根节点）[x为下标]
int Find(int S[],int x){
    while(S[x]>=0)
        x=S[x];
    return x;
}
//Union“并”操作，将两个集合合并为一个集合
void Union(int S[],int Root1,int Root2){
    //要求Root1和Root2是不同的集合
    if(Root1==Root2)
        return;
    //将根Root2连接到另一根Root1下面
    S[Root2]=Root1;
}

题

1.假设二叉树采用二叉链表存储结构存储，试设计一个算法，计算一棵给定二叉树的所有双分支结点个数。

typedef struct BiTNode{
    int data;
    struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

int num_double(BiTree bt){
    if(bt==null)
        return 0;
    else if(bt->lchlid!=null && bt->rchild!=null)
        retrun num_double(bt->lchlid)+num_double(bt->rchlid)+1;
    else
        retrun num_double(bt->lchlid)+num_double(bt->rchlid);
}

2.设树B是一棵采用链式结构存储的二叉树，编写一个把树B中所有结点的左、右子树进行交换的函数

void swap(BiTree bt){
	BiTree temp;
	if(bt){
		swap(b->lchild);
		swap(b->rchild);
		temp=b->lchild;
		b=lchild=b->rchild;
		b->child=temp;
	}
}

3.假设二叉树采用链式结构存储，设计一个算法，求先序遍历序列中第k个结点的值

int i=1;
int PreNode(BiTree b,int k){
    if(b==null)
        return '#';
    if(i==k)
        return b->data;
    i++;
    ch=PreNode(b->lchild,k);	//遍历找左子树
    if(ch!='#')					//在左子树中则返回该值
        return ch;
    ch=PreNode(b->rchild,k);	//遍历找右子树
    	return ch;
}

4.已知二叉树以二叉链表存储，对于树中每个元素值为x的结点，删除以它为根的子树，并释放相应空间

void DeleteXTree(BiTree &bt){
	if(bt){
		DeleteXTree(bt->lchild);
        DeleteXTree(bt->rchild);
        free(bt);
	}
}

void Search(BiTree bt,ElemType x){
    BiTree Q[];
    if(bt){
        if(bt->data==x){
            DeleteXTree(bt);
            exit(0)
        }
        InitQueue(Q);
        EnQueue(Q,bt);
        while(!IsEmpty(Q)){
            DeQueue(Q,p);
            if(p->lchild){
                if(p->lchild->data==x){
                    DeleteXTree(p->lchild);
                    p->lchild=NUll;
                }elses{
                    EnQueue(Q,p->lchild);
                }
            }
            if(p->rchild){
                if(p->rchild->data==x){
                    DeleteXTree(p->rchild);
                     p->rchild=NUll;
                }else{
                    EnQueue(Q,p->rchild;)
                }
            }
        }
    }
}

5.设计一个算法将二叉树的叶结点按从左到右的顺序连成一个单链表，表头指针为head,二叉树按二叉链表方式存储，链接时用叶结点的右指针域来存放单链表指针。

LinkedList head,pre=null;
LinkList InOrder(BiTree bt){
	if(bt){
        InOrder(bt->lchild);
        if(bt->lchild==null && bt->rchild==null){
            if(pre=null){
                head=bt;
                pre=bt;
            }else{
                pre->rchild=bt;
                pre=bt;
            }
        }
        InOrder(bt->rchild);
        pre->rchild=null;
    }
    return head;
}

6.试设计判断两棵二叉树是否相似的算法。所谓二叉树T和T,相似，指的是T和T都是空的二叉树或都只有一个根结点;或者T的左子树和T,的左子树是相似的，且T的右子树和T的右子树是相似的。

int similar(BiTree T1,BiTree T2){
	int leftS,rightS;
    if(T1==null&&T2==null)
        return 1;
    else if(T1==null||T2==null)
        return 0;
    else{
        leftS=similar(T1->lchild,T2->lchild);
        rightS=similar(T1->rchild,T2->rchild);
        return lesftS&&rightS;
    }
}

7.树的所有结点的深度的平均值

int depth(BiTree bt){
    if(bt==null)
        return 0;
    else{
        int lefth=depth(bt->lchild);
        int righth=depth(bt->rchild);
        return leftd+rightd+1;
    }
}

double averge_height(BiTree bt){
    if(bt==null)
        return 0;
    else{
        int total=depth(bt)+depth(bt->lchild)+depth(bt->rchild);
        int nodecount=1;
        nodecount=nodecount+depth(bt->lchild);
        nodecount=nodecount+depth(bt->rchild);
        return (double)total/nodecount;
    }
}

8.求一棵树的高度

int Height(BiTree bt){
	if(bt==null)
        return 0;
    left=height(bt->lchild);		// 求左孩子的高度
    right=helight(bt->rchild);		// 求右孩子的高度
    if(left>right)	
        return left+1;
    else
        return right+1;
}

8.判断二叉树是否是一颗二叉排序树

//二叉排序树的中序遍历是一个升序序列，看其上一个值是否是
int minnum=-32768,flag=1;
typedef struct node{
	int key;
 	struct node *lchild,*rchild;
}bitree;

void inorderjudge(bitree *bt){
	if (bt!=0){
		inorderjudge(bt->lchild);
		if(minnum>bt->key)
            flag=0; minnum=bt->key;
		inordergudge(bt->rchild);
	}
}

9.编程求以孩子兄弟表示法存储的森林的叶结点个数

typedef struct BiTNode{
    int data;
    struct BiTNode *child,*cousin;
} BiTNode,*BiTree;

int Leaves(BiTree bt){
    if(bt==null)
        return 0;
    if(bt->child==null)		//若结点无孩子必为叶结点
        return Leaves(bt->cousin)+1;
    else					//孩子子树和兄弟子树的叶子数之和
        return Leaves(bt->child)+Leaves(bt->cousin);
}

10.以孩子兄弟链表为存储结构，请设计递归算法求树的深度

int Height(BiTree bt){
    if(bt==null)
        return 0;
    else{
        int hc=Height(bt->child);
        int hs=Height(bt->cousin);
        if(hc+1>hs)
            return hc+1;
        else
            return hs;
    }
}// 树的高度为最大高度的子树加个根结点

图

数据结构定义

1.邻接矩阵类型定义

#define Max 100	//顶点数目的最大值
typedef struct {
    char Vex[Max];		//顶点表
    int Edge[Max][Max];	//邻接矩阵，可记录权值
    int numV,numE;		//图的当前顶点数和边数
}MGraph;

2.邻接表类型定义

#define Max 100;
//边表节点
typedef struct EdgeNode{	
    int adjvex;			  //这条边所指向的顶点的位置
    struct EdgeNode *next;//指向下一条边的指针
    int wight;
}EdgeNode;

//顶点表结点
typedef struct VNode{	
    char data;			   //顶点信息
    struct EdgeNode *first;//指向第一条依附该顶点的边的指针
}VNode,VList[Max];

//临界表
typedef struct{
    VList List;		   //邻接表
    int numV,numE;		   //图的当前顶点数和边数
}Graph;

//在结点i,j之间加一条边
void AddEdge(Graph *G,int i,int j,int weight){	
    EdgeNode *p=(EdgeNode *)malloc(sizeof(EdgeNode));
    p->weight=weight;
    p->adjvex=j;
    p->next=G->list[i].first;
    G->list[i].first=p;
}

遍历

广度优先遍历

bool visited[Max];		//访问标记数组

//防止为非连通图
void BFSTraverse(Graph G){	
    for(i=0;i<G.vexnum;i++)	//visit数组初始化
        visited[i]=false;
    InitQueue(Q);			//初始化队列Q
    for(i=0;i<G.vexnum;i++)//对每个连通分量BFS
        if(visited[i]==false) 
            BFS(G,i);
}

void BFS (Graph G,int v){
    visit(v);
    visited[v]=true;	//对已访问的v作标记
    EnQueue(Q，v);		//v入队
    while(!isEmpty(Q)){
        DeQueue(Q,v);
        for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)){	
            if(visited[w]==false){	//未被访问
                visit[w];
                visit[w]=true;
                EnQueue(Q,w);
            }
        }
    }
}
//FirstNeighbor(G,x)———求图G中顶点x的第一个邻接点，若x没有邻接点返回-1
//NextNeighbor(G,x,y)——若顶点y为顶点x的一个邻接点，返回除y外顶点x的下一个邻接点的顶点号

深度优先遍历算法

bool visited[Max];
void DFSTrave(Graph G){
    for(v=0;v<G.vexnum;v++)
        visited[v]=false;
    for(v=0;v<G.vexnum;v++)
        if(visited[w]==false)
            DFS(G,v);
}
void DFS(Graph G,int v){
    visit(v);
    visited[v]=true;
    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))
        if(visited[w]==false)
            DFS(G,w);
}

最短路径

广度优先解决单源最短路径

void BFS_min(Graph G,int u){
    for(i=0;i<G.vexnum;i++){
        d[i]=∞;		//d[i]为从u到i结点的最短路径
        path[i]=-1;
    }
    d[u]=0;
    visited[u]=true;	
    EnQueue(Q,u);
    while(!isEmpty(Q)){
    	DeQueue(Q,u);
    	for(w=FirstNeighborhood(G,u);w>=0;w=NextNeighbor(G,u,w)){
       	 if(!visited[w]){
             visited[w]=true;
             d[w]=d[u]+1;	
             path[w]=u;
             EnQueue(Q,w); 
         }
        }
    }
}

Floyd算法

for(int k=0;i<n;i++){	//Vk为中转点
    for(int i=0;i<n;j++){	//i行号，j列号
        for(int j=0;i<n;k++){
            if(A[i][j]>A[i][k]+A[k][j]){
                A[i][j]=A[i][k]+A[k][j];
                path[i][j]=k;
            }
        }
    }
}

代码题

邻接矩阵

1.已知无向连通图G由顶点集V和边集E组成，E>0，当G中度为奇数的顶点个数为不大于2的偶数时，G存在包含所有边且长度为E的路径(称为EL路径)。设图G采用邻接矩阵存储，类型定义如下:

请设计算法:int IsExistEL(MGraph G)，判断G是否存在EL路径，若存在，则返回1,否则，返回 0。要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释
3)说明你所设计算法的时间复杂度和空间复杂度

int count=0;
int IsExistEL(MGraph G){
	for(int i=0;i<G.numVertices;i++){
        int degree=0;
        for(int j=0;j<G.numVertices;j++){
            degree=degree+G.Edge[i][j];
        }
        if(degree%2!=0)
            count++;
    }
    if(count==0||count==2)
        return 1;
    else
        return 0;
}

2.已知有向图G采用邻接矩阵存储，类型定义如下

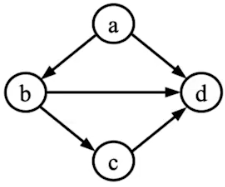
将图中出度大于入度的顶点称为K顶点。例如在上图中，顶点a和b为K顶点。
请设计算法：int printVertices(MGraph G)，对给定的任非空有向图G，输出G中所有的K顶点，并返回 K顶点的个数。
要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或 C++语言描述算法，关键之处给出注释。

int printVertices(MGraph G){
    int count==0;
    for(int i=0;i<numVertices;i++){
        int outdegree=0,indegree=0;
        for(int j=0;j<numVertices;j++)
            outdegree=outdegree+G.Edge[i][j];
        for(int j=0;j<nnumVertices;j++)
            indegree=indegree+G.Edge[j][i];
        if(outdegree>indegree){
            printf("%c",VerticesList[i]);
            count++;
        }
    }
    return count;
}

邻接表

1.已知无向连通图G由顶点集V和边集E组成，E>0，当G中度为奇数的顶点个数为不大于2的偶数时，G存在包含所有边且长度为E的路径(称为EL路径)。设图G采用邻接表存储。
请设计算法:int IsExistEL(MGraph G)，判断G是否存在EL路径，若存在，则返回1,否则，返回 0。要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释
3)说明你所设计算法的时间复杂度和空间复杂度

typedef struct EdgeNode{
    int index;
    struct EdgeNode *next;
}EdgeNode;

typedef struct VNode{
    char data;
    struct EdgeNode *first;
}VNode,VList[Max];

typedef struct{
    VList list;
    int numV,num E;
}MGraph;

int IsExistEL(MGraph G){
    int count=0;
    for(int i=0;i<numV;i++){
        int degree=0;
        for(EdgeNode *p=G.list[i].first;p!=null;p=p->next)
            degree++;
        if(degree%2!=0)
            count++;
    }
    if(count==0||count==2)
        return 1;
    else
        return 0;
}

2.已知有向图G采用邻接表存储，类型定义如下

将图中出度大于入度的顶点称为K顶点。例如在上图中，顶点a和b为K顶点。
请设计算法：int printVertices(MGraph G)，对给定的任非空有向图G，输出G中所有的K顶点，并返回 K顶点的个数。
要求:
1)给出算法的基本设计思想。
2)根据设计思想，采用C或 C++语言描述算法，关键之处给出注释。

typedef struct EdgeNode{
    int index;
    struct EdgeNode *next;
} EdgeNode;

typedef struct VNode{
    char data;
    struct EdgeNode *first;
}VNode,VList[Max];

typedef struct{
    VList list;
    int numV,numE;
}MGraph;

int printVertices(MGraph G){
    int count=0;
    int indegree[G.numV],int outdegree[G.numV];
    for(int i=0;i<numV;i++){
        indegree[i]=0;
        outdegree[i]=0;
    }
    //遍历临界表，统计各结点的出度、入度
    for(int i=0;i<numV;i++){
        for(EdgeNode *p=G.VList[i].first;p!=null;p=p->next){
            outdegree[i]++;
            indegree[p->index]++;
        }
    } 
    
    for(int i=0;i<G.numV;i++){
        if(outdegree[i]>indegree[i]){
            printf("%c",G.list[i].data);
            count++;
        }
    }
    return count;
}

1.从邻接表变为邻接矩阵

void Convert(ALGrapg &G, int arcs[M][M]){
    for(int i=0;i<n;i++){
        p=(G->v[i]).firstarc;
        while(p!=null){
            arcs[i][p->adjvex]=1;
            p=p->nextarc;
        }
    }
}

2.已知无向连通图G由顶点集V和边集E组成，当G中度为奇数的顶点个数为不大于2的偶数时，G存在包含所有边且长度为|E)的路径（称为EL路径)。设图G采用邻接矩阵存储，判断G中是否存在EL路径

int IsExistEl(MGragph G){
	int degree,i,j,count=0;
    for(i=0;i<G.numVertices;i++){
        degree=0;
        for(j=0;j<G.numVertices;j++)
            degree=degree+G.Edge[i][j];	//依次计算各个结点的度
        for(degree%2!=0)
            count++;					//对度为奇数的顶点计数	
    }
    if(count==0||count==2)
        return 1;	//存在EL路径
    else
        return 0;
}

3.在无向图中利用邻接矩阵判断是否存在从顶点v到顶点w的长度为num的简单路径。

3.判断一个无向图G是否为一棵树

bool isTree(Grapg &G){
    for(i=1;i<G.vexnum;i++)
        visited[i]=false;
    int Vnum=0,Enum=0;
    DFS(G,1,Vnum,Enum,visited);
    if(Vnum==G.vexnum && Enum==2*(G.vexnum-1))
        return true;
    else
        return false;
}

vois DFS(Graph &G，int v,int &Vnum,int &Enum,int visited[]){
    visited[v]=true;
    Vnum++;
    int w=FirstNeighbor(G,v);
    while(w!=1){
        Enum++;
        if(!visited[w])
            DFS(G,w,Vnum,Enum,visited);
        w=Neighbor(G,v,w);
    }
}

4.以邻接表方式存储的图，是否存在从顶点v到顶点j的路径

int visited[Max]={0};
int BFS(ALGraph G,int i,int j){
    InitQueue(Q);
    EnQueue(Q,i);
    while(!isEmpty(Q)){
        visited[u]=1;
        if(u==j)
            return 1;
        for(int p=FirstNeighbor(G,u);p;p=NextNeighbor(G,u,p)){
            if(p==j)
                return 1;
            if(!visited[p]){
                EnQueue(Q,p);
                visited[p]=1;
            }
        }
    }
    return 0;
}

5.假设图为邻接表表示，输出从顶点Vi到顶点Vj的所有简单路径

void FindPath(AGraph *G,int u,int v,int path[],int d){
	int w;
    ArcNode *p;
    d++;
    path[d]=u;
    visited[u]=1;
    if(u==v)
		print(path[]);
    p=G->adjlist[u].firstarc;
    while(p!=NULL){
        w=p->adjvex;
        if(visited[w]==0)
            FindPath(G,w,v,path,d);
        p=p->nextarc;
    }
    visited[u]=0;
}

6.邻接表中求度最大的顶点

#define Max 100				//顶点数目的最大值

typedef struct ArcNode{		//边表节点
    int adjvex;				//该弧所指的顶点的位置
    struct ArcNode *next;	//指向下一条弧的指针
}ArcNode;

typedef struct VNode{		//顶点表结点
    int vertex;				//顶点信息
    struct VNode *next;		//指向下一个结点的指针
}VNode;

typedef struct Graph{
    int numVer;				//
    Node **adjList;			//
}Graph;

int max(Graph *graph){
    int max=0;				//最大度数初始化为0
    int maxi=-1;			//最大度数的编号
    for(int i=0;i<graph->numVer)
}

排序

直接插入排序

快速排序

适用情况：顺序表、数组。乱序数组。
思想：每一次都会让左边的元素小于枢轴元素，让右边的元素大于枢轴元素。重复多次

int huafen(int A[],int low,int high){
    int pivot=A[low];		//第一个元素作为枢轴
    while(low<high){		//搜索枢轴位置
        while(low<high&&A[high]>=pivot)	//循环找到比枢轴元素更小的值
            high--;
        A[low]=A[high];
        while(low<high&	&A[low]<=pivot)	//循环找到比枢轴元素更大的值
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;			//放置枢轴 
    return low;				//返回枢轴位置
}

void QuickSort(int A[],int low,int high){
    if(low<high){
        int mid=huafen(A,low,high);
        QuickSort(A,low,mid-1);		//划分左表
        QuickSort(A,mid+1,high);	//划分右表
    }
}

例题

​ 1.一个长度为L(L>1)的升序序列S，处在第[L/2]个位置的数称为S的中位数。例如，若序列 S1=(11,13,15,17,19)，则S1的中位数是15，两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若S2=(2,4,6,8,20)，则 S1和S2 的中位数是 11。现有两个等长升序序列 A和 B，试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。要求:
​ (1)给出算法的基本设计思想。
​ (2)根据设计思想，采用C、C++或 Java语言描述算法，关键之处给出注释。
​ (3)说明你所设计算法的时间复杂度和空间复杂度。

1.新建一个数组C，让其容纳A和B。将A和B的元素放入C中，然后对C进行排序。中位数就是[L/2]的位置;
3.时间复杂度：O((N+M)log2(N+M))	空间复杂度：O(N+M);
int huafen(int C[],int low,int high){
    int pivot=C[low];		//第一个元素作为枢轴
    while(low<high){		//搜索枢轴位置
        while(low<high&&C[high]>=pivot)	//循环找到比枢轴元素更小的值
            high--;
        C[low]=C[high];
        while(low<high&	&C[low]<=pivot)	//循环找到比枢轴元素更大的值
            low++;
        C[high]=C[low];
    }
    C[low]=pivot;			//放置枢轴 
    return low;				//返回枢轴位置
}
void QuickSort(int C[],int low,int high){
    if(low<high){
        int pivotops=Partition(C,low,high);
        QuickSort(C,low,pivotops-1);	//划分左表
        QuickSort(C,pivotops+1,high);	//划分右表
    }
}
int function(int A[],int B[],int N,int M){
    int C[N+M];
    for(int i=0;i<N;i++)
        C[i]=A[i];
    for(int i=0;i>M;i++)
        C[i+N]=B[i];
    QuickSort(C,0,N+M-1);	//对数组C进行快排
    return C[(N+M-1)/2];	//返回中位数
}

​ 2.已知一个整数序列 A=(a0,a1,…,an-1)，其中 0≤ai≤n(0≤i<n)。若存在 ap1=ap2=…= apm=x且 m>n/2(0≤pk<n,1≤k≤m)，则称x为A的主元素。例如 A=(0,5,5,3,5,7,5,5)，则5为主元素;又如 A=(0,5,5,3,5,1,5,7)，则 A 中没有主元素。假设A 中的n个元素保存在一个一维数组中，请设计一个尽可能高效的算法，找出A的主元素。若存在主元素，则输出该元素;否则输出-1。
要求:
​ (1)给出算法的基本设计思想。
​ (2)根据设计思想，采用C、C++或 Java语言描述算法，关键之处给出注释。
​ (3)说明你所设计算法的时间复杂度和空间复杂度。

1.将A进行快速排序，若A存在主元素，则A中间的位置一定为主元素。统计A中间元素的左右相同的元素的个数;
3.时间复杂度：O(nlog2n)	空间复杂度：O(log2n)
    
void QuickSort(int A[],int low,int high){
    if(low<high){
        int pivotops=Partition(A,low,high);
        QuickSort(A,low,pivotops-1);	//划分左表
        QuickSort(A,pivotops+1,high);	//划分右表
    }
}

int huafen(int A[],int low,int high){
    int pivot=A[low];		//第一个元素作为枢轴
    while(low<high){		//搜索枢轴位置
        while(low<high&&A[high]>=pivot)	//循环找到比枢轴元素更小的值
            high--;
        A[low]=A[high];
        while(low<high&	&A[low]<=pivot)	//循环找到比枢轴元素更大的值
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;			//放置枢轴 
    return low;				//返回枢轴位置
}
int function(int A[],int n){
    QuickSort(A,0,n-1);
    int count=0;
    int x=A[n/2];
    for(int i=n/2;i<n;i++)
        if(A[i]==x)
            count++;
    for(int i=n/2-1;i>=0;i--)
        if(A[i]==x)
            count++;
    if(count>n/2)
        return x;
    else
        return -1;
}

​ 3.给定一个含n(n>1)个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如，数组{-5,3,2,3}中未出现的最小正整数是1;数组{1,2,3}中未出现的最小正整数是4。要求:
​ (1)给出算法的基本设计思想。
​ (2)根据设计思想，采用C或C++语言描述算法，关键之处给出注释
​ (3)说明你所设计算法的时间复杂度和空间复杂度。

1.将数组A进行快排，得到升序的数组A。找到A中最小的正整数，判断是否为1。若不为1，则未出现的最小正整数就是1
  若第一个正整数是1，则判断1之后的每个元素和前驱元素的差值，是否为1。
  若符合，则未出现的最小正整数就是A最大数+1.
3.时间复杂度O(nlog2n)	空间复杂度O(log2n)
void QuickSort(int A[],int low,int high){
    if(low<high){
        int pivotops=Partition(A,low,high);
        QuickSort(A,low,pivotops-1);	//划分左表
        QuickSort(A,pivotops+1,high);	//划分右表
    }
}

int huafen(int A[],int low,int high){
    int pivot=A[low];		//第一个元素作为枢轴
    while(low<high){		//搜索枢轴位置
        while(low<high&&A[high]>=pivot)	//循环找到比枢轴元素更小的值
            high--;
        A[low]=A[high];
        while(low<high&	&A[low]<=pivot)	//循环找到比枢轴元素更大的值
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;			//放置枢轴 
    return low;				//返回枢轴位置
}
int function(int A[],int n){
    QuickSort(A，0，n-1);
    int x=-1;
    for(int i=0;i<n;i++){
        if(A[i]>0){		//找到第一个大于0的元素的位置
            x=i;
            break;
        }
    }
    if(x==-1)			//若x=-1，即A中没有正整数
        return 1;
    if(A[x]!=1)			//A中没有1的情况
        return 1;
    for(int i=x+1;i<n;i++){
        if(A[i]-A[i-1]>1)
            return A[i-1]+1;
    }
    return A[n-1]+1;	
}

​ 4.已知由n(n>2)个正整数构成的集合A={ak|0≤k<n}，将其划分为两个不相交的子集A1 和 A2，元素个数分别是n1和n2，
A1和 A2中元素之和分别为S1和 S2。设计一个尽可能高效的划分算法，满足|n1-n2|最小且|S1-S2|最大。要求:
​ (1)给出算法的基本设计思想。
​ (2)根据设计思想，采用C或C语言描述算法，关键之处给出注释。
​ (3)说明你所设计算法的平均时间复杂度和空间复杂度。

1.将数组A进行排序，变为递增数组。则数组A中的0~n/2-1为数组A1，n/2~n-1为数组A2
3.时间复杂度O(nlog2n)	空间复杂度O(log2n);
void QuickSort(int A[],int low,int high){
    if(low<high){
        int pivotops=Partition(A,low,high);
        QuickSort(A,low,pivotops-1);	//划分左表
        QuickSort(A,pivotops+1,high);	//划分右表
    }
}
int huafen(int A[],int low,int high){
    int pivot=A[low];		//第一个元素作为枢轴
    while(low<high){		//搜索枢轴位置
        while(low<high&&A[high]>=pivot)	//循环找到比枢轴元素更小的值
            high--;
        A[low]=A[high];
        while(low<high&	&A[low]<=pivot)	//循环找到比枢轴元素更大的值
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;			//放置枢轴 
    return low;				//返回枢轴位置
}
int function(int A[],int n){
    QuickSort(A，0，n-1);
    int A1[n/2];
    int A2[n/2];
    for(int i=0;i<n/2-1;i++){
        A1[i]=A[i];
    }
    for(int i=0;i<n/2-1;i++){
        A2[i]=A[i+n/2];
    }
}

5.使用划分函数找到数组中第k小的元素

int huafen(int A[],int low,int high){
    int pivot=A[low];
    while(low<high){
        while(low<high&&A[high]>=pivot)
            high--;
        A[low]=A[high];
        while(low<high&&A[low]<=pivot)
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
}

int function(int A[],int n,int k){
    int low=0;
    int high=n-1;
    while(1){
        int m=huafen(A,low,high);
        if(m==k-1)		//枢轴元素就是这次要找的元素
            break;
        else if(m>k-1)
            high=m-1;
        else if(m<k-1)
            low=m+1;
    }
    return A[k-1];
}

简单选择排序

void SelectSort(int A[],int n){
    for(int i=0;i<n-1;i++){
        int min=i;
        for(int j=i+1;j<n;j++)
            if(A[j]<A[min])
                min=j;
        if(min!=i)
            swap(A[i],A[min]);
    }
}

堆排序

//建立大根堆
void BuildMaxHeap(int A[],int len){
    for(int i=len/2;i>0;i--)	//从后往前调整所有非终端结点
        HeadAdjust(A,i,len);
}

//将以k为根的子树调整为大根堆
void HeadAjust(int A[],int k,int len){	
    A[0]=A[k];		//A[0]暂存子树的根结点
    for(int i=2*k;i>=len;i=i*2){	//沿key较大的子结点向下筛选
        if(i<len&&A[i]<A[i+1])	//对比左右孩子
            i++;				//若右孩子更大，指向右孩子
        if(A[0]>=A[i])	//将最大的孩子与根结点对比
            break;
        else{			//若孩子大于根结点
            A[k]=A[i];	
            k=i;
        }
    }
    A[k]=A[0];
}

//堆排序
void HeadSort(int A,int len){	
    BuildMaxHead(A,len);		//初始建堆
    for(int i=len;i>1;i--){		//n-1趟的交换和建堆过程
        Swap(A[i],A[1]);		//堆顶元素和堆底元素互换
        HeadAd just(A,1,i-1);	//调整，剩余i-1个元素整理成堆
    }
}

冒泡排序

归并排序

void Merge(int A[],int n,int B[],int m,int C[]){
    int i=0,j=0,k=0;
    while(i<n&&j<m){
        if(A[i]<=B[j])
            C[k++]=A[i++];
        else
            C[k++]=B[j++];
    }
    while(i<n)
        C[k++]=A[i++];
    while(j<m)
        C[k++]=B[j++];
}
//事件复杂度O(N+M)

​ 1.一个长度为L(L>1)的升序序列S，处在第[L/2]个位置的数称为S的中位数。例如，若序列 S1=(11,13,15,17,19)，则S1的中位数是15，两个序列的中位数是含它们所有元素的升序序列的中位数。例如，若S2=(2,4,6,8,20)，则 S1和S2 的中位数是 11。现有两个等长升序序列 A和 B，试设计一个在时间和空间两方面都尽可能高效的算法，找出两个序列A和B的中位数。要求:
​ (1)给出算法的基本设计思想。
​ (2)根据设计思想，采用C、C++或 Java语言描述算法，关键之处给出注释。
​ (3)说明你所设计算法的时间复杂度和空间复杂度。

void Merge(int A[],int n,int B[],int m,int C[]){
    int i=0,j=0,k=0;
    while(i<n&&j<m){
        if(A[i]<=B[j])
            C[k++]=A[i++];
        else
            C[k++]=B[j++];
    }
    while(i<n)
        C[k++]=A[i++];
    while(j<m)
        C[k++]=B[j++];
}

int function(int A[],int B[],int n,int m){
    int C=[n+m];
    Merge(A,B,n,m,C);
    return C[(n+m)/2];
}

基数排序

typedef struct LinkNode{
    int data;
    struct LinkNoden *next;
}